
Hiện tượng này không phải là phép màu hay sự ngẫu nhiên đơn thuần, mà hoàn toàn có thể được lý giải dựa trên quy luật toán học của lịch Gregory (Dương lịch) mà chúng ta đang sử dụng. Quy luật này dựa trên chu kỳ lặp lại của các ngày trong tuần theo năm.
Một năm thông thường có 365 ngày. Khi chia 365 cho 7 (số ngày trong một tuần), ta được 52 tuần và dư 1 ngày (365 = 52 x 7 + 1). Điều này có nghĩa là nếu một ngày cụ thể (ví dụ: ngày 1/1) của năm nay là thứ Hai, thì sang năm sau (nếu không phải năm nhuận), ngày đó sẽ là thứ Ba (tiến lên 1 ngày).
Tuy nhiên, cứ 4 năm một lần, chúng ta lại có một năm nhuận với 366 ngày (thêm ngày 29/2). Năm nhuận có 52 tuần và dư 2 ngày (366 = 52 x 7 + 2). Điều này làm cho ngày trong tuần của năm kế tiếp nhảy cách 2 ngày so với năm nhuận trước đó (tính từ tháng 3 trở đi).
Sự kết hợp giữa các năm thường (dư 1 ngày) và năm nhuận (dư 2 ngày) tạo ra một chu kỳ lặp lại của lịch. Chu kỳ phổ biến nhất để lịch lặp lại hoàn toàn là 28 năm (7 ngày/tuần x 4 năm/chu kỳ nhuận). Tuy nhiên, còn có các chu kỳ khác như 6 năm, 11 năm, 12 năm, tùy thuộc vào vị trí các năm nhuận trong khoảng thời gian đó.
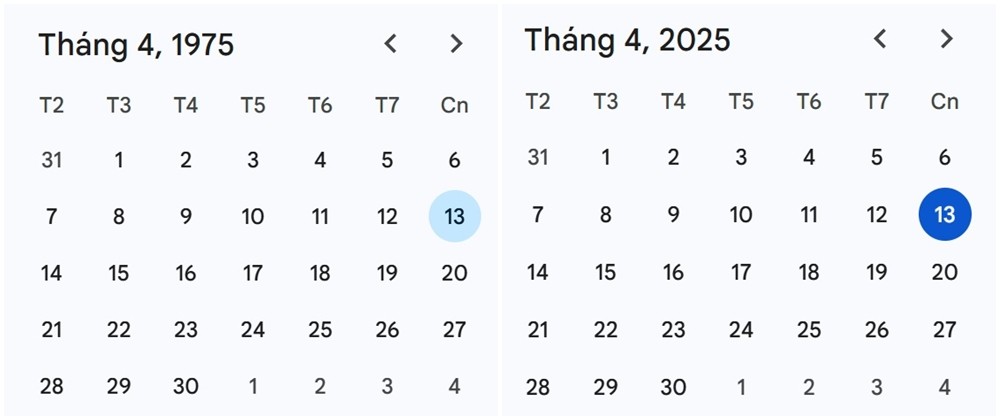
Khoảng cách giữa năm 1975 và 2025 là đúng 50 năm. Trong 50 năm này, có tổng cộng 13 năm nhuận (1976, 1980, 1984, 1988, 1992, 1996, 2000, 2004, 2008, 2012, 2016, 2020, 2024). Tổng số ngày trong 50 năm này là: (50 năm x 365 ngày/năm) + 13 ngày nhuận = 18250 + 13 = 18263 ngày.
Điều kỳ diệu nằm ở chỗ: 18263 chia hết cho 7 (18263 / 7 = 2609). Chính vì tổng số ngày trong 50 năm này là một bội số của 7, nên các ngày trong tuần của tháng 4/2025 sẽ lặp lại y hệt như tháng 4/1975.
Sự trùng hợp toán học này, diễn ra đúng vào cột mốc 50 năm ngày thống nhất, như một lời nhắc nhở thú vị về dòng chảy của thời gian và tính chu kỳ của lịch sử. Nó không làm thay đổi ý nghĩa trọng đại của sự kiện, nhưng chắc chắn đã thêm một nét chấm phá đặc biệt, khiến cho dịp kỷ niệm nửa thế kỷ ngày non sông liền một dải càng trở nên đáng nhớ hơn.














